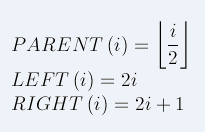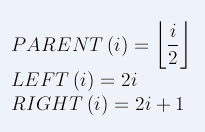- A+
1.概述
堆排序(Heap Sort)就是利用堆(假设利用大顶堆)进行排序的方法。
原理:将待排序的序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根结点,将 它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的次小值。,如此反复执行,便能得到一个有序序列了,堆排序的时间复杂度为O(nlogn)。
1.1 什么是堆
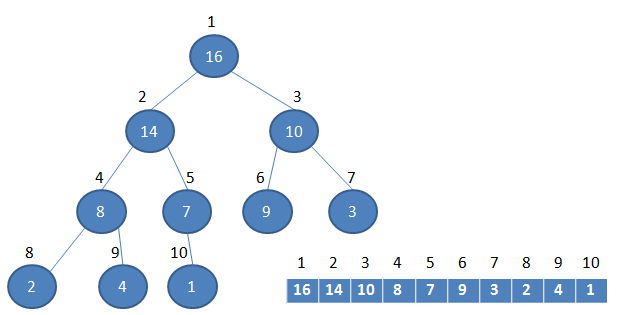
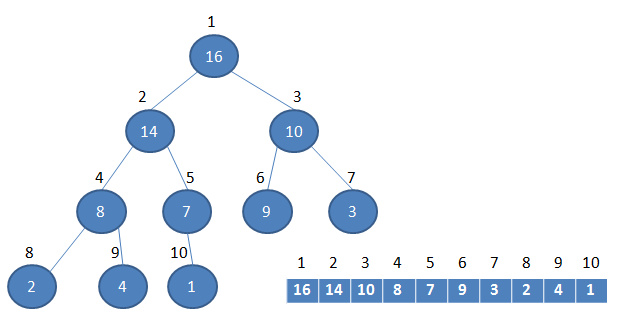
这里的堆(二叉堆),指得不是堆栈的那个堆,而是一种数据结构。堆可以视为一棵完全的二叉树,完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示,每一个结点对应数组中的一个元素.
数组与堆之间的关系
二叉堆一般分为两种:最大堆和最小堆。
1.2 什么是最大堆
堆中每个父节点的元素值都大于等于其孩子结点(如果存在),这样的堆就是一个最大堆,因此,最大堆中的最大元素值出现在根结点(堆顶)
1.3 节点与数组索引关系
对于给定的某个结点的下标i,可以很容易的计算出这个结点的父结点、孩子结点的下标,而且计算公式很漂亮很简约
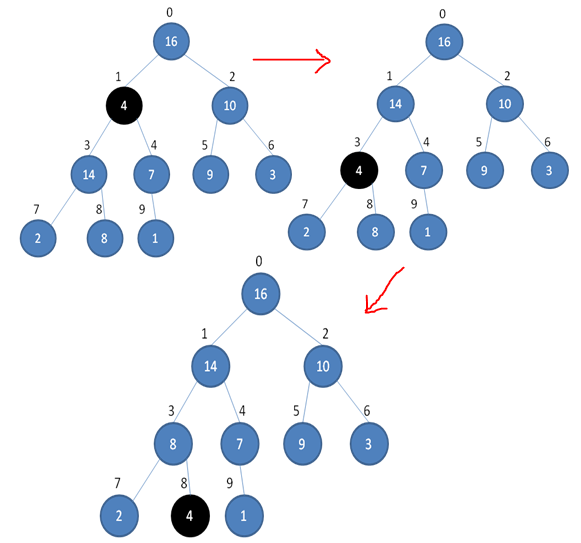
1.4 调整过程
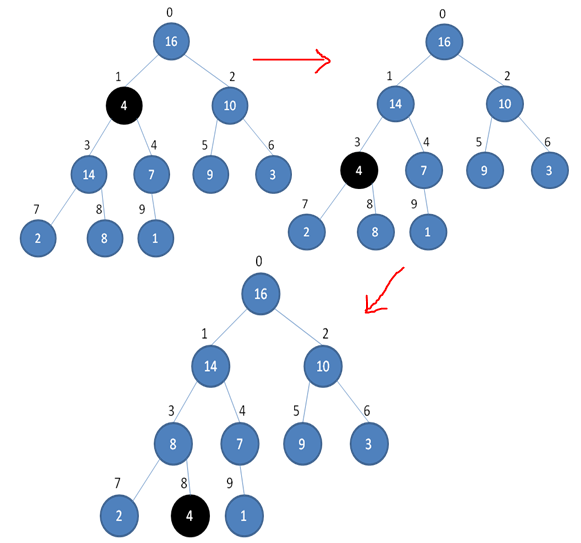
在4,14,7这个小堆里边,父节点4小于左孩子14,所以两者交换,在4,2,8这个小堆里边,父节点4小于右孩子8,所以两者交换
上图展示了一趟调整的过程,这个过程递归实现,直到调整为最大堆为止。
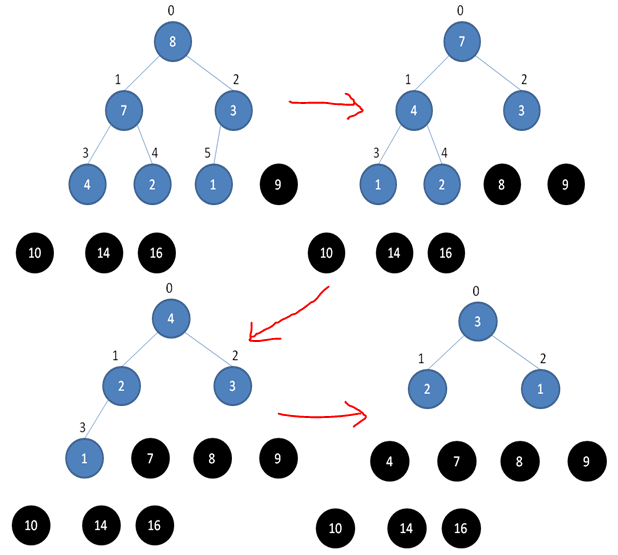
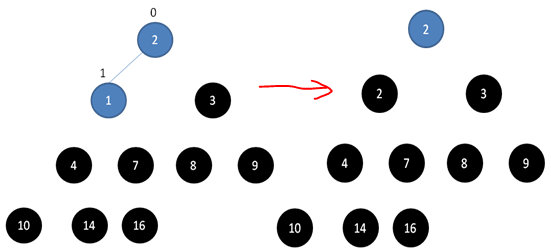
1.5 整个堆排序过程
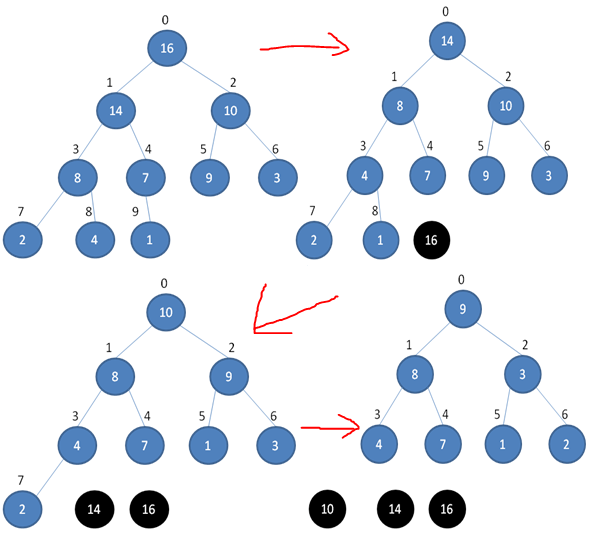
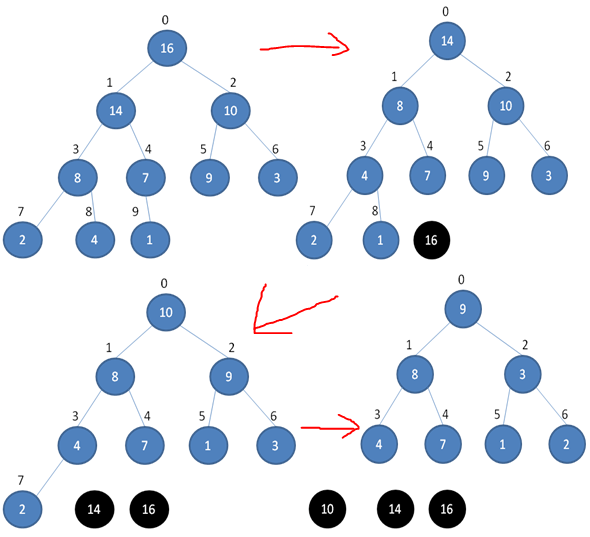
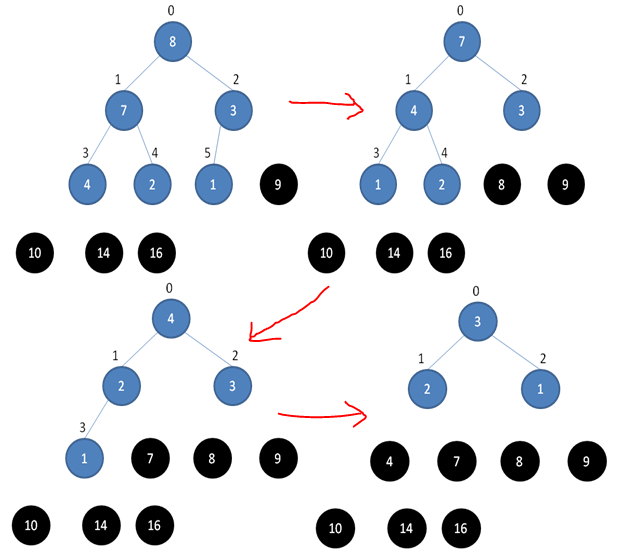
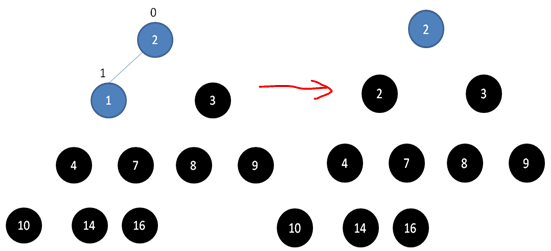
堆排序就是把堆顶的最大数取出,将剩余的堆继续调整为最大堆,以递归实现,剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束。下边三张图详细描述了整个过程。
2.示例
//堆排序 public static void HeapSort(int[] arr) { BuildMaxHeap(arr); for (int i = (arr.Length - 1); i > 0; i--) { //将堆顶元素和无序区的最后一个元素交换 int temp = arr[i]; arr[i] = arr[0]; arr[0] = temp; MaxHeaping(arr, 0, i); //将新的无序区调整为堆 } } /// <summary> /// 初始化大根堆,由底向上建堆 /// 完全二叉树的基本性质,最底层节点是n/2,所以从arr.Length/2开始 /// </summary> private static void BuildMaxHeap(int[] arr) { for (int i = (arr.Length / 2) - 1; i >= 0; i--) { MaxHeaping(arr, i, arr.Length); } } /// <summary> /// 将指定的节点调整为堆 /// </summary> /// <param name="i">需要调整的节点</param> /// <param name="heapSize">堆的大小,也指数组中无序区的长度</param> private static void MaxHeaping(int[] arr, int i, int heapSize) { int left = 2 * i + 1; // 左子节点 int right = 2 * i + 2; // 右子节点 int large = i; // 临时变量,存放大的节点值 if (left < heapSize && arr[left] > arr[large]) { large = left; } // 比较右子节点 if (right < heapSize && arr[right] > arr[large]) { large = right; } // 如有子节点大于自身就交换,使大的元素上移 if (i != large) { int temp = arr[i]; arr[i] = arr[large]; arr[large] = temp; ; MaxHeaping(arr, large, heapSize); } } // int[] list = new[] { 16, 14, 10, 8, 7, 9, 3, 2, 4, 1 }; // Sorter.HeapSort(list);
参考:http://blog.kingsamchen.com/archives/547#viewSource
1.概述
堆排序(Heap Sort)就是利用堆(假设利用大顶堆)进行排序的方法。
原理:将待排序的序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根结点,将 它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的次小值。,如此反复执行,便能得到一个有序序列了,堆排序的时间复杂度为O(nlogn)。
1.1 什么是堆
这里的堆(二叉堆),指得不是堆栈的那个堆,而是一种数据结构。堆可以视为一棵完全的二叉树,完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示,每一个结点对应数组中的一个元素.
数组与堆之间的关系
二叉堆一般分为两种:最大堆和最小堆。
1.2 什么是最大堆
堆中每个父节点的元素值都大于等于其孩子结点(如果存在),这样的堆就是一个最大堆,因此,最大堆中的最大元素值出现在根结点(堆顶)
1.3 节点与数组索引关系
对于给定的某个结点的下标i,可以很容易的计算出这个结点的父结点、孩子结点的下标,而且计算公式很漂亮很简约
1.4 调整过程
在4,14,7这个小堆里边,父节点4小于左孩子14,所以两者交换,在4,2,8这个小堆里边,父节点4小于右孩子8,所以两者交换
上图展示了一趟调整的过程,这个过程递归实现,直到调整为最大堆为止。
1.5 整个堆排序过程
堆排序就是把堆顶的最大数取出,将剩余的堆继续调整为最大堆,以递归实现,剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束。下边三张图详细描述了整个过程。
2.示例
//堆排序 public static void HeapSort(int[] arr) { BuildMaxHeap(arr); for (int i = (arr.Length - 1); i > 0; i--) { //将堆顶元素和无序区的最后一个元素交换 int temp = arr[i]; arr[i] = arr[0]; arr[0] = temp; MaxHeaping(arr, 0, i); //将新的无序区调整为堆 } } /// <summary> /// 初始化大根堆,由底向上建堆 /// 完全二叉树的基本性质,最底层节点是n/2,所以从arr.Length/2开始 /// </summary> private static void BuildMaxHeap(int[] arr) { for (int i = (arr.Length / 2) - 1; i >= 0; i--) { MaxHeaping(arr, i, arr.Length); } } /// <summary> /// 将指定的节点调整为堆 /// </summary> /// <param name="i">需要调整的节点</param> /// <param name="heapSize">堆的大小,也指数组中无序区的长度</param> private static void MaxHeaping(int[] arr, int i, int heapSize) { int left = 2 * i + 1; // 左子节点 int right = 2 * i + 2; // 右子节点 int large = i; // 临时变量,存放大的节点值 if (left < heapSize && arr[left] > arr[large]) { large = left; } // 比较右子节点 if (right < heapSize && arr[right] > arr[large]) { large = right; } // 如有子节点大于自身就交换,使大的元素上移 if (i != large) { int temp = arr[i]; arr[i] = arr[large]; arr[large] = temp; ; MaxHeaping(arr, large, heapSize); } } // int[] list = new[] { 16, 14, 10, 8, 7, 9, 3, 2, 4, 1 }; // Sorter.HeapSort(list);
参考:http://blog.kingsamchen.com/archives/547#viewSource